June 2022: Wouter Deleersnyder
Flexible, wavelet-based inversion within the SimPEG framework
Abstract¶
The salinization map of the region of Flanders, Belgium shows the depth of the interface between fresh and salt groundwater in the coastal and polder area. It serves as an exploratory tool to examine the potential of groundwater projects that improve freshwater availability in the shallow subsurface. Flanders environment agency published an updated map in 2019, based on airborne time-domain electromagnetic induction data. The result of the inversion is, however, overly smooth, which potentially conceals interesting features.
Via an inverse problem, the electromagnetic induction data can be mapped onto a conductivity profile, which serves as a proxy for salinity via petrophysical laws. The inverse problem is ill-posed and regularization improves the stability of the inversion. Based on Occam’s razor principle, a smoothing constraint is typically used with a very large number of thin layers. However, the salinity profiles in the Belgian coastal plains are sometimes sharp, impeding the correct estimation of the fresh-saltwater interface. In practice, the real underground might be either blocky or smooth, or somewhere in between. Standard constraints are thus not always appropriate.
With our novel wavelet-based inversion scheme, the original time-domain AEM data can be re-interpreted in a flexible fashion, meaning that we can easily generate an ensemble of inversion models with different types of Occam's razor minimum-structure. The flexibility is due to the wavelet basis. In simple terms, a wavelet function can be seen as a building block and a simple model is one that can be built with few building blocks of various sizes. Our proposed inversion scheme adds a regularization term that limits the number of building blocks in the wavelet-domain to make sure only the necessary complexity is retrieved. The scale-dependency makes the use of small blocks more expensive, as it corresponds to adding detail. The scheme is tuned by only one additional parameter (which determines the wavelet basis function) and can recover blocky, intermediate and smooth structures. It is also capable to recover high amplitude anomalies in combination with globally smooth profiles, a common problem for smooth inversion, and an essential feature to accurately predict the salinity.
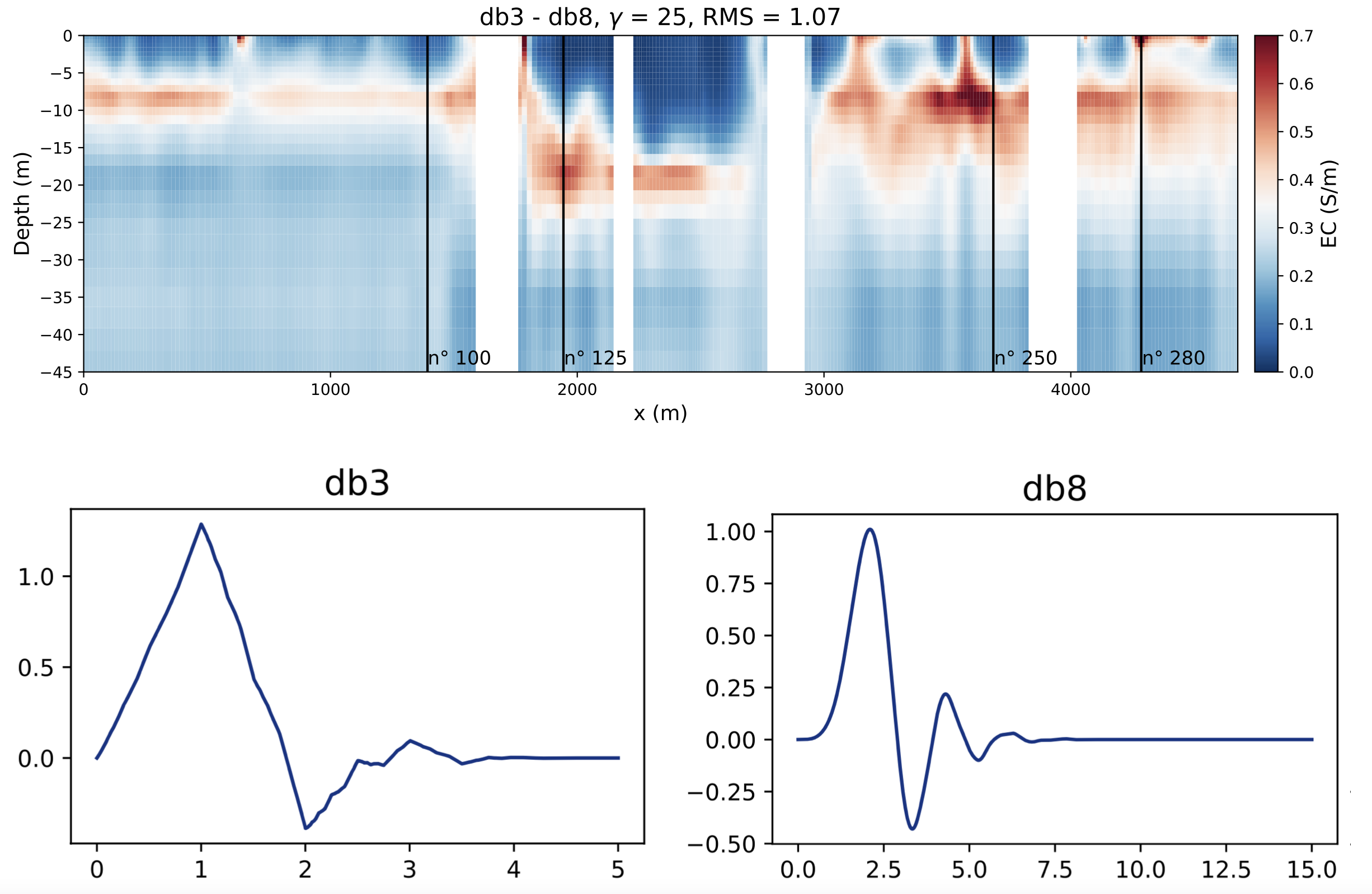
Inversion model generated with the flexible, scale-dependent wavelet-based regularization scheme with the db3 wavelet basis along the vertical orientation and the db8 wavelet basis along the horizontal orientation. The features of the wavelet basis (e.g., sharpness) loosely correspond to the constraints imposed on the inversion model.
We first demonstrated this alternative inversion scheme on 1D FDEM data Deleersnyder , 2021 and now extend it to 2D AEM data a in a saltwater intrusion context Deleersnyder , 2022. The flexibility of the method allows for choosing the appropriate sharpness for each orientation. In Figure 1, an inversion model is shown with a relatively sharp wavelet basis (db3) in the vertical orientation, while a smoother wavelet basis (db8) is used along with the lateral orientation. Imposing the appropriate sharpness on the inversion model is crucial to obtaining a reliable estimation of the fresh-saltwater interface.
The code behind the 1D regularization has been adjusted to the SimPEG framework and is open to everyone Deleersnyder & Thibaut, 2022. This allows to use this flexible regularization term for many types of inversion problems and promotes geoscience reproducibility!
Bio¶

Wouter Deleersnyder is a passionate Ph.D. candidate at the physics department of KU Leuven and Geology department of Ghent University. With his technical skills from his physics education (Master in Physics, KU Leuven, Belgium in 2019), he wants to tackle the problems of today. Stimulated by the importance of water for man and nature, he came into contact with groundwater and geophysics. He is working on new methods to get a better picture of what is under the ground. He is specializing in electromagnetic induction surveys, forward modelling, inversion, and uncertainty quantification.
- Deleersnyder, W., Maveau, B., Hermans, T., & Dudal, D. (2021). Inversion of electromagnetic induction data using a novel wavelet-based and scale-dependent regularization term. Geophysical Journal International, 226(3), 1715–1729. 10.1093/gji/ggab182
- Deleersnyder, W., Maveau, B., Dudal, D., & Hermans, T. (2022). Flexible quasi-2D inversion of time-domain AEM data, using a wavelet-based complexity measure. 10.48550/ARXIV.2205.06458
- Deleersnyder, W., & Thibaut, R. (2022). WouterDls/1D-wavelet-based-inversion: Wavelet Based Inversion. Zenodo. 10.5281/ZENODO.6552695